 One listmate asked me about how I keep my brain from falling asleep after having gotten a master's degree in Operations Research (statistics) and done nothing with it. For the past two weeks, making math calculations for my new crochet project has kept my mind occupied. Believe it or not, I found the need to manipulate and factor a polynomial in making calculations for a crocheting project! Algebra and crocheting????
One listmate asked me about how I keep my brain from falling asleep after having gotten a master's degree in Operations Research (statistics) and done nothing with it. For the past two weeks, making math calculations for my new crochet project has kept my mind occupied. Believe it or not, I found the need to manipulate and factor a polynomial in making calculations for a crocheting project! Algebra and crocheting???? Yes, read on . . .
If you dare . . .
(Maniacal laughter in the background) . . .
Issue 1:
I am crocheting a 75" by 90" afghan to cover (and protect) my dear husband's leather couch with the same diagonal stitch used in my recent baby blanket project. The yarn I plan to use is colored by dye lot. If I fail to buy the right number of skeins, I will waste money by having too many skeins or fall short of my intended size or buy yarn from a different dye lot and end up with slightly different tints from one skein to the next. I bought one skein of the yarn I planned to buy in bulk, crocheted the diagonal stitch until I run out of yarn, and calculated the area in square inches. With the number, I guestimated how many skeins are needed to make 6,750 square inches (75" x 90").
 To have a double check, I calculated the area of the triangle pictured above made from one skein in two ways:
To have a double check, I calculated the area of the triangle pictured above made from one skein in two ways:* I measured the sides that would form a square made of this diagonal. I found the area of the square and divided by two: 21x21/2 = 220.5 square inches/skein.
* I measured the hypotenuse (the diagonal) and the base (which cuts the triangle in symmetrical halves) and divided by two: 30x14.5/2 = 217.5 square inches/skein.
To reach 6,750 square inches, I would need 31 skeins, so I bought 32 to make it even:
Total number of skeins = 6,750 square inches/220.5 square inches/skein
= 30.6 skeins
OR
Total number of skeins = 6,750 square inches/217.5 square inches/skein
= 31.0 skeins
Issue 2:
I find it fun to measure my progress by calculating the number of blocks I have completed (one block = ch 2, 3 dc) at the end of each row. The first row begins with one block; the second row, two blocks; the third row, three blocks; etc.
Row 1: 1 = 1
Row 2: 1 + 2 = 3
Row 3: 1 + 2 + 3 = 6
I could have figured it out in Excel by making a spreadsheet and printing it out a chart through 150 rows. But then, I remembered there were formulas for things like this. I played around with the numbers and spotted the following pattern:
Row N: 1 + 2 + . . . + N = N(N+1)/2
I even proved it to myself to make sure it was right, but such a proof goes beyond the scope of this blog (tee, hee, hee).
 Issue 3:
Issue 3:This formula came in handy when I was trying to figure out what to do with my lone skein with its lone dye lot. I decided to make a mat for an Rock Garden Steve bought for his office. In Issue 1, I had made a triangle with 34 rows plus 10 surplus blocks and ended up with 605 blocks for the entire skein:
Total number of blocks = 34(35)/2 + 10
= 17(35) + 10
= 595 + 10
= 605
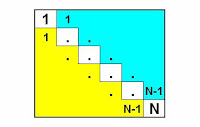 I wanted to make the mat as large as possible, but only wanted to rip back to the half way point. To calculate the number of blocks in the middle row of my mat of unknown size, I drew the illustration pictured left. If that middle row has N blocks (white blocks), the row before it (the yellow half) has N-1 blocks as does the row after it (the blue half). To calculate the total number of blocks in a square mat with N blocks along the diagonal, I add the number of blocks in the white row plus the number blocks in the yellow half to the number of blocks in the blue half:
I wanted to make the mat as large as possible, but only wanted to rip back to the half way point. To calculate the number of blocks in the middle row of my mat of unknown size, I drew the illustration pictured left. If that middle row has N blocks (white blocks), the row before it (the yellow half) has N-1 blocks as does the row after it (the blue half). To calculate the total number of blocks in a square mat with N blocks along the diagonal, I add the number of blocks in the white row plus the number blocks in the yellow half to the number of blocks in the blue half:Total Number of Blocks = White + Yellow + Blue
Using the formula from issue, I get:
Total Number of Blocks = N + (N-1)(N-1 + 1)/2 + (N-1)(N-1 + 1)/2
= N + (N-1)N/2 + (N-1)N/2
= N + (N-1)N(1/2 + 1/2)
= N + (N-1)N
= N + N*N - N
= N*N
I must have my total number of blocks less than 605, and it must be a whole number!
N*N < 605 N*N - 605 = 0 (N + 24.6)(N - 24.6) = 0 Since N must be a whole, I round it down to 24, which means I must rip back to the row with 24 blocks. Was I right? Yes! When I finished the mat, only a tiny ball of yarn remained. Issue 4:
I wondered how many blocks will be in the longest row of this blanket. If I get 605 blocks per skein, I should end up with 19,360 blocks in all:
Total number of blocks = 32 skeins x 605 blocks/skein
= 19,360 blocks.
Using the formula used in the third issue, I calculate there will be 139 blocks in the longest row:
N*N < 19,360
N*N - 19,360 = 0
(N + 139.14)(N - 139.14) = 0
Whoever said you would never use this stuff in real life?
Class dismissed!

4 comments:
I loved this post, though, not being too mathematically inclined, it hurt my brain. I could follow the steps if I had to.
I knit, but these blanket photos make me want to learn to crochet. The colors in the mat are beautiful. Is that a rock garden fountain?
Hoo Boy, Tammy. Alan could sure go faster in math if he had you for a teacher instead of me! He told his Ph. D. holding Dad that only I could teach Saxon math. What a laugh!
I'm glad you do something with all your learning. Me? I am not learning how to do a box and whisker plot I have not needed until now.
Yes, that is a rock garden fountain with some supplementary shells. The colors are called painted desert (Red Heart Super Saver, Economy Size).
Mary, my math skills did me no good with Mr. Random (David). For years, he has struggled with math. It is only in the past three months that he has caught on, and it's about time because he is taking Algebra this year! I do not remember doing box and whiskers until I took statistic courses for my bachelor's degree. They expect kids to learn way more than we did!
I just finished the blanket. To be safe I ordered an extra skein and had just under one skein to spare. Yep, math works, people!!!
Post a Comment